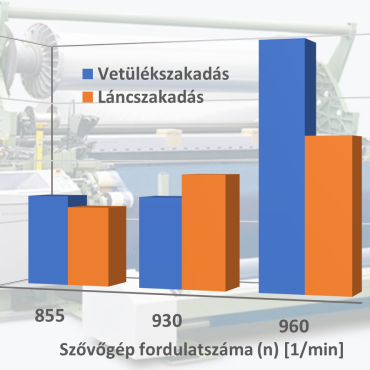
Amióta a textiliparban, azon belül a szövödékben tevékenykedem, nem hagy nyugodni a gondolat, hogy megértsem és leírjam a többgépes kiszolgálás (szövő – szövőgép, fonó – fonógép, stb.) folyamatát.
Az érdeklődésemet első sorban a téma „megközelíthetetlensége” okozta és okozza a mai napig. Sok forrásból sokféle megoldási módszert ismerhettem meg. A fontosabbak:
- Lugosi Károly: Többgépes rendszerek termelékenységének és gazdaságosságának elemzése, TMTE kiadás, 1962. (Áttekintést ad a kérdéskörről, hivatkozik az első (1933), e témában megjelent közlésre, felsorolja a különböző szerzők különféle megközelítését, végül kiválasztja Ashcroft: The Productivity of Several Machines Under the Care of One Operator, Journal of Royal Statitical Society, 1950. leírását, mint követendőt)
- Вентцель Е.С.: Теория вероятностей. Москва, Наука, Физматгиз, 1969
- Leonard Kleinrock: Queuing Systems. Vol I: Theory (Magyarul: Sorbanállás – kiszolgálás. Bevezetés a tömegkiszolgálási rendszerek elméletébe. Műszaki Könyvkiadó, Budapest, 1979.)
- Robert c. Meier, William T. Newell, Harold L. Pazer: Simulation in business and economics. (Magyarul: Szimuláció a vállalati gazdálkodásban és a közgazdaságtanban, Közgazdasági és Jogi Kiadó, Budapest, 1973.)
Lugosi (ld. fent) gyakorlatban kialakult módszerként írja le, hogy a szövő munka normaszámításánál a szövőállásba beszerelt cikkek összetételétől függetlenül minden egyes szövetre meghatározták a „terhelés mértékét”. Tették ezt oly módon, mintha az összes kezelt gépen ugyanazt a terméket állították volna elő. A szövő leterhelését a szövőállásra beszerelt ezen értékek összege adta meg. Az elvárt teljesítmény pedig az ehhez tartozó követelmény volt. Ez volt a normaszámítás lényege, s egyben a bérezés alapja is.
Ezt már akkor nagyon igazságtalan és rossz eljárásnak tartottam, hisz ha egy-egy szövőgépen munkaigényesebb szövet előállítása vált szükségessé, a szövő által kezelt gépcsoport mérhető teljesítménye a számítottat meghaladónál kisebb lett. Ezzel a munkavégzőben ellenérdekeltség alakult ki. A nehezebben „szőhető” cikkektől mindenki szabadulni akart. Ezt gyakran a mesterek ki is használták, kivételeztek a kedvencekkel, nekik adták a könnyebben szőhető lánchengereket.
A fenti hibás megközelítés miatt az üzemi vezetőség részéről is hamis állásfoglalás alakulhatott ki.
- Állították, hogy a szövő „leterhelését” 100 százalékosra kell beállítani a kezelt gépek számának megváltoztatásával. Üldözték az „alul terheltséget”.
- A kezelt gépekre beszerelt cikkcsoport által generált terhelés egy-egy „rosszabb” lánchenger beszerelése után – értékelésük szerint – 100 százalék fölé is nőhetett. Sajnos az ily módon kiszámolt termelékenység mindig meghaladta a tényleges értéket. Ennek következtében teljesítési elmaradás következett be, s a keresetcsökkenés miatt kialakuló dolgozói stressz tovább rontotta az üzem helyzetét.
Az üzemben folyó munka hatékonyságának ilyen alapon történő megítélése csak hibás következtetésekhez vezethetett. A helytelen gyakorlat valószínű az volt, hogy lehetetlen volt leírni a folyamatot.
A fentiek inspiráltak az összefüggések mélyebb megismerésére. A diplomatervem elkészítésekor (1971) találkoztam először a sztochasztikus folyamatok fogalmával. Bizonyságot szereztem róla, hogy ennek az eszköztárnak az alkalmazása vihet csak közelebb e szituáció leírásához is.
Több sikertelen kísérlet után a tudásom elmélyítésével jutottam el e leírás lehetőségéhez. A cikk témája a leírás felvázolása lesz.
Elméleti alapok (technicus terminus)
Az egy kezelő által kiszolgált több egység kiszolgálási rendszert alkot. A kiszolgálási rendszereknek az alapja néhány fogalom. Ezek:
- a kiszolgált (kezelt) egységek (gépek, orsók) és a kiszolgáló csatornák (gépkezelők, szövők, fonók) száma
- a bemeneti folyamat – esetünkben a kiszolgált szövőgépek, fonógépek leállásainak egymásutánja
- a kiszolgálási folyamat – a kiszolgáló (gépkezelő, pl. szövő) által végrehajtott beavatkozások (szakadás elhárítás, anyag utánpótlás, vakleállás elhárítása, stb) folyamata.
Mindkét folyamatot az időbeni gyakoriságukkal jellemezzük. A kiszolgálási folyamat esetén beszélünk átbocsátó képességről is. Ez a kiszolgáló egység véges kapacitása, amivel ki tudja elégíteni a rendszerbe érkező igényeket.
Az ilyen módon leírt folyamatok összessége a kiszolgálási folyamat. Ennek két formáját különböztetjük meg.
- Az egyik az, amikor a beérkező igények mindig azonos időközönként jelennek meg a bemeneten s a kiszolgálás is minden esetben azonos időtartam alatt történik meg. Az ilyen folyamatot diszkrétnek nevezzük.
- Ha az igények beérkezése és/vagy a kiszolgálás időtartama nem egyenletes, a folyamat neve: sztochasztikus (véletlenszerű) folyamat.
Belátható, hogy az általunk vizsgálni óhajtott folyamatok mindegyike sztochasztikus.
Ha gyakoriság-felvételt készítünk a beérkezési és a kiszolgálási folyamatokról, a kapott értékek eloszlása akár folyamatonként is különböző lesz. Úgy mondjuk, hogy mind a beérkezési, mind a kiszolgálási folyamatokat valószínűségi fogalmakkal, az átlagértékkel, az értékek szórásával és az eloszlásfüggvénnyel írhatjuk le.
A folyamatot az előre nem jelezhető időpontokban megjelenő kiszolgálási igény és a kiszolgálás időtartamának véletlenszerűsége jellemzi. Könnyű belátni, hogy ilyen esetekben előfordulhat, hogy a kiszolgáló csatorna még foglalt egy igény kiszolgálásával, amikor már megjelenik a bemeneten a következő igény. Természetesen utóbbinak várakoznia kell, amíg a megelőző igény kiszolgálása be nem fejeződik. Ezt a várakozást nevezzük sorban állásnak.
A várakozó igények száma gyakran nem növelhető minden határ nélkül. Emiatt be kell vezetnünk a befogadó képesség fogalmát is.
A folyamat leírására, a mennyiségi jellemzők meghatározására a sorbanállás-elmélet eszköztárát tudjuk felhasználni. A kiszolgálási rendszereket aszerint csoportosíthatjuk, hogy hány beérkezési és hány kiszolgáló csatorna található bennük, s a beérkezési és kiszolgálási folyamatok eloszlása melyik eloszlásfüggvénnyel írható le.
A textiliparban használatos további jellemzők, amelyekkel a későbbiekben operálunk:
- A szakadékonyság. Mértékegysége az 1/100 000 vetés (fordulat).
- A hatásfok, a gép időkihasználása, azaz a működési idő és az időalap viszonya.
Az alapfogalmak tisztázása után lássuk a probléma megoldás lehetséges módjait!
A tömeg-kiszolgálási rendszerek (TR) jelölés-rendszere
A rendszerek megkülönböztetésére az egyszerűbb és egységes hivatkozás miatt szabványos jelölésrendszert alakítottak ki. A jelölés egy ’/’ jelekkel elválasztott betűsorból áll.
- Az első betű, ami mindig nagybetű, a beérkező igények eloszlásának jelölésére szolgál. Általában három eloszlástípust különböztetnek meg, úgymint
- általános (G) (general),
- Markov (M) és
- diszkrét (D) eloszlást.
Lehetőség van egyéb eloszlások megjelölésére is (pl. Erlang, lognormális, egyenletes, normál, stb.).
- A második betű a kiszolgálás időtartamának eloszlását írja le. A megkülönböztetett eloszlástípusok megegyeznek az első betűnél felsoroltakkal.
- A harmadik érték a kiszolgáló csatornák számát adja meg. A további jelek el is maradhatnak, vagy a helyükön nincs megjelölés.
- A negyedik jel a rendszer befogadó képességét írja le.
- Az ötödik jel az igénypopuláció számát adja meg. A zárt kiszolgálási rendszerekben ez az igényforrások száma. Például a szövő munkánál ez a kezelt gépek száma.
A fentiek bemutatására írjunk le két rendszert!
- Legyen ez a szövő munkavégzése. A gondjaira bízott gépek száma legyen N. A bemeneti és kiszolgálási időtartamok eloszlása legyen tetszőleges (G). A rendszer jelölése:
G/G/1//N.
- Ha a leállások folyamata Poisson folyamat, azaz a gépek teljesen véletlenszerűen állnak le, a szövőállásban két szövő dolgozik, s a javítást mindig azonos időtartam alatt végzik el, a rendszer:
M/D/2//N.
Be kell még vezetnünk néhány szabványos jelölést, amit a szakirodalom következetesen alkalmaz.
- Az igények beérkezésének gyakorisága λ (1/időegység), tehát a beérkezések közötti átlagos időtartam 1/λ.
- A kiszolgálás ’sebessége’ μ (1/időegység), azaz a beavatkozás átlagos időtartama 1/μ.
- A két gyakoriság hányadosa ρ=λ/μ, a kiszolgálási tényező. (Ez a mennyiség kötelezően kisebb 1-nél).
Ezeknek a fogalmaknak a használata valószínű némi idegenkedést vált ki, de ahhoz, hogy valamilyen megoldást tudjunk találni a felvetett problémakörre, elengedhetetlen hogy ezt az eszközrendszert használjuk, a szabványos jelöléseket alkalmazzuk.
A zárt TR ábrázolása és leírása. (Ventcel idézett könyve alapján.)
A továbbiakban a legegyszerűbb rendszert, az M/M/1//N rendszert vizsgáljuk. Ebben a rendszerben lehet a működés stabil állapotában olyan jellemzőket meghatározni λ < μ esetére, viszonylag hosszú időtartamra, amelyek matematikai megoldást adhatnak. Bonyolultabb esetekben ez nem mindig lehetséges. A munkásból és n gépből álló rendszer több állapotban lehet. Ezeket az állapotokat mi az álló gépek számával fogjuk jelölni, azaz
- S0 – minden gép működik, a munkás szabad.
- S1 – egy gép áll, a munkás a javításával van elfoglalva.
- S2 – két gép áll, egy javítás alatt van, a másik ’sorban áll’ várva a javításra.
- …
- SN –az összes gép áll, egy javítás alatt van, N-1 pedig ’sorban áll’.

A rendszert az S0 állapotból az S1 állapotba az összes gép meghibásodási rátája (nλ) viszi át; az S1-ből az S2-be már csak n-1 gép által generált ráta hat, mert már csak n-1 gép működik; s így tovább. Ami viszont az állapotok közti történő ellenkező irányú haladást illeti, ott a gyakoriság végig egyforma (μ), hisz végig egy munkás dolgozik, azonos intenzitással.
A folyamat – mivel véletlenszerű – csak az állapotok valószínűségének határértékeivel írható le. Ez hosszabb időtávú megfigyeléssel határozható meg, amint ezt a gyakorlat is bizonyítja (pl. szakadásfelvétel).
A megmaradás elvének felhasználásával felírható, mivel az állapotokba be és kimenő folyamatok egyensúlyban vannak (a továbbiakban a gépek számát N-nel jelöljük):
Az S1 állapotra felírhatjuk: bemenet: Nλ az S0, μ az S2 felől, illetve kimenet: μ az S0 felé és (n-1)λ az S2 felé. Az eljárás az összes állapotra folytatható. Végül az adott állapotban tartózkodás valószínűségére a következő egyenletrendszer adódik:
p1 = Nλ/μ · p0
p2= N(N-1)λ2/μ2 · p0
···
pN= N(N-1)(N-2) ··· λN/μN · p0,
és mivel a rendszer valamilyen állapotban mindig van, így
p0 + p1 + ··· + pN = 1 (1)
Az egyenletrendszert p0-ra megoldva:
p0 = [1 + Nλ/μ + N(N-1)(λ/μ)2 + ··· + N(N-1) ··· 1(λ/μ)N]-1
Felhasználva a már felírt összefüggést a kiszolgálási tényezőre, az egyenlet a következőképp egyszerűsödik:
p0 = [1 + Nρ + N(N-1)ρ2 +···+ N(N-1) ··· 1ρN]-1 (2)
Ily módon az állapotok valószínűsége az egyéb jellemzőkből meghatározható:
p1 = Nρp0
p2 = N(N-1)ρ2p0
···
pN = N(N-1) ··· 1ρNp0
Az „abszolút áteresztő képesség” szerepét az adott esetben a munkás által egységnyi idő alatt elhárított hibák száma adja. Számítsuk ki ezt a jellemzőt.
A munkás elfoglaltsága:
Pelfoglaltság = 1 – p0
Ha a kiszolgáló (pl. a munkás) foglalt, akkor μ hibát hárít el időegységenként, azaz az abszolút áteresztő képesség
A = (1 – p0)μ
Annak valószínűsége, hogy a munkás nem lesz elfoglalt
Pszabad = 1 – Pelfoglalt = p0
Számítsuk ki az álló gépek, azaz a kiszolgálással érintett gépek számát. Jelöljük ezt W-vel. Ez a mennyiség közvetlenül számítható az alábbi összefüggésből:
W = 1p1 + 2p2 + ··· + NpN
Egyszerűbb meghatározni W-t az abszolút áteresztő képességből (A). Mivel minden működő gép λ intenzitású meghibásodási folyamatot generál, a vizsgált TR-ben átlagosan N-W gép működik, aminek az átlagos meghibásodási rátája (N-W)λ, s minden meghibásodást elhárít a munkás, tehát
(N – W)λ = (1 – p0)μ ;
ahonnan
W = N – μ/λ(1 – p0), vagyis
W = N – (1 – p0)/ρ
Most határozzuk meg a sorban álló gépek számát (R)! A következőképpen okoskodunk: a kiszolgálással kapcsolatos gépek száma (W) egyenlő a sorban álló gépek (R) és a kiszolgálás alatt lévő gépek (Ω) számának összegével, azaz
W = R + Ω
A kiszolgálás alatt lévő gépek száma 1, ha a munkás foglalt, egyébként 0 (ha a munkás tétlen), azaz Ω átlagos értéke annak valószínűsége, hogy a munkás foglalt
Ω = 1 – p0
Kivonva ezt a mennyiséget a kiszolgálással elfoglalt gépek számából, kapjuk
R = W – Ω = [N – (1 – p0)/ρ] – (1 – p0).
Állapodjunk meg még egy jellemzőn, a munkás által kiszolgált gépcsoport termelés veszteségén:
L = Wt = [N – (1 – p0)ρ] · l,
ahol l a fajlagos termelékenységi érték.
Most írjuk át a kapott jellemzőket a textiles gyakorlat nyelvére. A gépek hatásfokának (η) nevezzük tulajdonképpen azok munkaidő kihasználtságát
η = (1 – p0)/ρN = t/ρN (3)
Ily módon tehát a gépek hatásfokát (időkihasználását) egzakt összefüggésbe hoztuk a működést leíró egyéb jellemzőkkel. Az utolsó összefüggés alkotó elemei
- p0: annak valószínűsége, hogy minden gép üzemel és a munkás tétlen
- t = 1 – p0: a szövő leterhelése
- ρ: a kiszolgálási tényező, azaz a meghibásodások gyakoriságának és a hibaelhárítás intenzitásának a hányadosa
- N: a kezelt gépek száma
Ismételten megjegyezzük, hogy bármilyen elegáns, a fenti levezetés és megoldás csak mind az igények, mind azok kiszolgálásának teljes véletlensége (az M/M/1//N rendszerre) esetén igaz.
Bármily kecsegtető is, hogy egy viszonylag egyszerű összefüggést találtunk a gépcsoport működésére, sajnos a gyakorlatban ez általában nincs így. A dolgok véletlensége – gondoljunk csak a hibaelhárítási időkre – nem teljesül. Azok középérték(ek) körül csoportosulnak.
Ennek ellenére vizsgálódásokat végezhetünk erre a modellre is, – mert mint a folytatásban megmutatjuk – a rendszerek viselkedése hasonló.
A modell vizsgálata
A vizsgálatok során általában nem egy állapotot elemzünk, hanem tágabb paraméter tartományra terjesztjük ki érdeklődésünket. Adódik a feladat, hogy ábrázoljuk a kapott összefüggésünket grafikusan. Ez részben az említett elemzést is segíti, ugyanakkor számoló ábrát ad a szakemberek kezébe. (Így nincs szükség a textiles számára idegen terminológia elsajátítására és a kapcsolódó számítások elvégzésére.)
A fenti összefüggés alapján elkészített diagramok (nomogramok) az
η = f(N, ρ)
p0 = φ(N, ρ)
függvény szerint készíthetők el. (Elkészítjük előtte az értéktáblákat is.) Kiegészítjük ezt a jellemzők (λ és ρ) grafikus kiszámításával is. A kiszolgálási tényező (ρ) meghatározásához összefüggés:
ρ = λ / μ.
A meghibásodási ráta (λ) a szakadékonysággal (ε) hozható összefüggésbe. A gondot az okozza, hogy a meghibásodási ráta időegységre vonatkozik, míg a szakadékonyságot hagyományosan 100 ezer vetésre (100 ezer fordulatra) ismerjük. Az időegységre (min) jutó vetésszám egyúttal a szövőgép fordulatszáma (n). Az összefüggés tehát
λ = 100 000 ε/n [1/min]
A szövő beavatkozásainak elfogadott értéke egy tapasztalati érték. A Sulzer Bulletinben publikált adatok széles körűen elfogadottak, ezért mi is ezeket használjuk a következőkben:
- tarkán szövés illetve bonyolult szövésnél 24 – 36 beavatkozás óránként
- egyszerű szövés esetén 48 – 56 beavatkozás óránként.
A hibaelhárítási ráta (a beavatkozás gyakorisága) elvárt értékét hivatott biztosítani a szövők képzése (pl. az ipari tanuló képzés és/vagy a munkaszervező cégek [Werner, Czipin, stb.] nyújtotta képzés). Természetesen ez az érték a személytől, a munkakörülményektől, stb. is függ, de van egy elvárt érték.
Példánkban gondot okoz még a munkás tétlenségének (p0) meghatározása az összefüggésből. Ehhez számítógépes algoritmust célszerű készíteni. Alakítsuk át az eredeti matematikai kifejezést egy rekurzív megoldási algoritmussá:
z = [(…(((0 + 1)ρ + 1)·2ρ + 1) ··· )·(N – 1)ρ + 1]·Nρ + 1
p0 = z-1
A hatásfokösszefüggése: η = (1 – p0)/ρN
A számítási algoritmus a következő (Basic):
N, i integer
p0, ρ, η real
Értékadás ->N és ρ ->N, ρ kiíratása
p0 = 1
for i = 1 to N
p0 = ρ·i·p0
p0 = p0 +1
next
p0 = 1 / p0 ->p0 kiíratása
η = 1 – p0
η = η / Nρ ->η kiíratása
A fenti módon meghatározott értékhalmazból (aminek egy szeletét az alábbi táblázat tartalmazza) diagramot (monogramot) készíthetünk.


A független változónak (x tengely) a kiszolgálási tényezőt választottuk. A diagramok alatt a ρ = λ / μ értékek meghatározását lehetővé tevő számoló ábrát helyeztük el, mellette pedig a szakadékonyság és a gépfordulat összefüggésének nomogramját.
Megjegyzendő, hogy a modern szövőgépeken számítógépes adatgyűjtés is van (régebben pl. a Loomdata, ma pedig a gépek fedélzeti számítógépe). Ennek adatai (fordulatszám, beavatkozás/fordulat, beavatkozás/időegység) közvetlenül felhasználhatók a számításoknál.
Hosszabb időszak vizsgálata alapján azon szövőket, akik az elvárt teljesítményt nem érik el, oktatni kell. Az elvárt értéknél jobb eredményt elérő szövők munkamódszerét, időbeosztását tanulmányozva alakítható ki a gyengébbek oktatásának tudásbázisa.
Következtetések
- Bemutattuk a többgépes kiszolgálás jellemzői közti analitikus összefüggéseket a legegyszerűbb, a Markov folyamatokat tartalmazó rendszerre.
- Ennek alapján, a szükséges adatok meghatározásán át, bemutattuk az elmélet gyakorlati felhasználásának lehetőségét (nomogram).
- Ráirányítottuk a figyelmet a munkavégzés emberi tényezőinek vizsgálatára, az ebből nyerhető gyakorlati eredményekre.
Ezeket az eredményeinket csak fenntartással szabad alkalmazni, ugyanis – nem lehet elégszer hangsúlyozni, hogy – az érvényességük az egyszerűsítések (ideális eloszlások feltételezése) miatt korlátozott.
Sajnos a leírtakhoz hasonló egzakt matematikai megoldásokat a tetszőleges eloszlású bemeneti és munkavégzési folyamatok esetére még nem találtak.
Más módszerekhez kell folyamodni, hogy általánosságban is elemezhető legyen a rendszer. De előtte néhány példa a nomogram használatához
- A szakadékonyság ε= 30/100 000 vetés, a szövőgép fordulatszáma 300/min.
Leolvasható, hogy a meghibásodási gyakoriság 1,67/h. Ez 20/h beavatkozási sebességnél a kiszolgálási tényező 0,082 értékének felel meg.
6 gép kezelése esetén a munkás tétlensége 0,56, tehát a terhelése 44 %-os. A gépcsoport hatásfoka 89 %.
- A gépcsoport hatásfoka 90 %, a kezelt gépszám 4. Milyen feltételek mellett kapunk ilyen eredményt
A kiszolgálási tényező 0,08. Ha a gépek fordulatszáma 300/perc és a szövő 20 beavatkozást tud elvégezni óránként, a szakadékonyság 30/100 000 vetés.
Ha a szakadásfelvétel alapján a szakadékonyság 40/100 000 vetés, a szövő munkavégzési sebessége kb. 30 beavatkozás óránként.
- Hány gépet tud kiszolgálni a szövő 40/100 000 vetés szakadékonyság és 400/min gépfordulatszám mellett?
Ha a szövő munkavégzési sebessége 50/h, 0,77-es tétlenség (23 % terhelés) mellett a kezelhető gépszám 8, 20/h munkavégzési sebesség esetén a kiszolgálási tényező 0,077 értékű, ami 0,45 arányú tétlenség (55 %-os leterhelés) esetén 4 gép kezelését teszi lehetővé.
Megjegyezzük, hogy a szakirodalom szerint a szövő terhelését 50 – 70 %-os tartományban kell tartani, mert ekkor várható el megfelelő minőségű munkavégzés. A 100 %-os terhelés illúzió, hisz a szövő az időegységre eső beavatkozásai lecsökkentésével lecsökkenti a terhelését is. Ez (bizonyos határok között) egy önszabályozó folyamat.
A nem véletlenszerű (nem Markov folyamattal modellezhető) folyamatok vizsgálata
További elemzéseinket a korábbi törekvések elemzésével folytatjuk. Ezek arra irányultak, hogy a teljesen véletlenszerű folyamatok mellett a gyakorlatban tapasztalható, ettől eltérő eloszlásokra történő alkalmazások is leírhatókká váljanak.
1. Az irodalomjegyzékben szereplő könyvben Lugosi Károly olyan megoldást javasol, hogy a kiszolgálási idők véletlenszerű és diszkrét eloszlására is meghatározza a folyamat jellemzőit. Feltételezi, hogy a gyakorlatban előforduló eloszlás a teljesen véletlenszerű (Markov) és a mindig azonos idejű (Discret) eloszlás közé esik. A két érték által meghatározott jellemzőket, mint szélső értékeket alkalmazva becsli meg a valós jellemzőket. Egy diagramot közöl a Markov és a diszkrét eloszlású kézi időkkel számított jellemzők különbségére. Ezt a diagramot, átvéve az eredeti forrásból, alább közöljük mi is. (itt a kiszolgálási tényezőt ρ helyett p jelöli). A számítási módszert homály fedi.

Látható, hogy a legnagyobb eltérés a két eloszlással jellemezhető folyamat közt a 70 – 90 %-os terhelési tartományban van. Értéke 1,5 – 6 % közötti.
A fenti megközelítés közelebb visz bennünket a tényleges helyzet leírásához, azonban feltételezi a meghibásodási folyamat teljes véletlenszerűségét. A gyakorlatban ez az elméleti állapot azonban nem mindig áll fenn, s az sem igaz mindig, hogy a kézi idők eloszlása a feltételezett tartományba esik.
Az eltéréseket tényleges idő-felvételezéssel is lehet igazolni. Erre gondolatban is következtethetünk, ha figyelembe vesszük, hogy a szakadékonyságon kívül a darabvételek, a hengercserék és a műszaki meghibásodások egyaránt befolyásolják a meghibásodási folyamatot, amelyek eloszlását nem mindig lehet egy sokaságba összevonni. Sőt a szakadékonyság is két alapvető tényezőtől, a lánc- és vetülékfonalak szakadékonyságától függ. Akkor még nem beszéltünk a vakleállásokról és a vetülékcsere gyakoriságának befolyásáról.
A másik probléma, hogy a fenti gyakoriságok sok, egymástól független, közel azonos súlyú tényező egyidejű hatása alatt állnak. A valószínűség elmélet ilyen esetekre a logaritmikus normális (lognormális) eloszlást valószínűsíti. Ezt legtöbbször szakadásfelvételekkel is igazolni lehet.
Lugosi a fentebb említett egyéb, a szakadásoktól eltérő jelenségeket konstansok beiktatásával igyekszik leírni, felosztva a gépek működési idejét különféle szakaszokra. A megközelítés eléggé mesterkéltnek tűnik, s az elméletének alkalmazhatósága úgy érhető el, hogy tényleges időfelvétellel kapott eredményeket húzzuk rá az elméle szerinti értékekre.
2. Meg kell még említenünk a Sulzer publikációkban és tanfolyamokon bemutatott módszert. A szövés gazdaságosságát elemző gondolatmenet alapját az alábbi összefüggés adja:
A prof. Dale Jones eljárás leírását a Lugosi könyve tartalmazza (22-25. oldal). A használhatóságát csak vakon fogadhatjuk el.
3. Ennyi áttekintés után (miután több eszmefuttatást nem sikerült fellelni) állítjuk, hogy nem tudjuk elfogadható módon leírni a valódi, természetes folyamatot. Valami más módszert kell találni a probléma megoldására.
Erre szolgáltat módszert a modellezés
A számítástechnika fejlődése adott egy, a gyakorlatban rendkívül könnyen alkalmazható, rugalmas megoldást a folyamat leírására – a szimulációt (modellezést). A számítógépen lejátsszuk a folyamatot, s megfelelő időegységnyi (pl. egy műszak vagy egy munkanap) futtatás után meghatározzuk a folyamat jellemzőit.
A felépített modell különféle szituációk vizsgálatát is lehetővé teszi, mindössze a bemeneti paramétereket kell megváltoztatni.
A szimuláció egy szimulációs programozási nyelv segítségével valósítható meg. Ez a GPSS programnyelv. A következőkben röviden bemutatjuk ezt a szimulációs eszközt a Wikipédia szócikke alapján. (Lásd még a Szimuláció a vállalati gazdálkodásban és a közgazdaságtanban című könyv 265.-272. oldalain)
GPSS egy olyan szimulációs nyelv, amelyet különböző rendszerek, főleg tömegszolgálási rendszerek szimulálására használnak. A GPSS rendszert az IBM alkalmazottja Jeffrey Gordon fejlesztette ki 1961-ben . Gordon létrehozta a nyelv öt első változatát: GPSS (1961), GPSS II (1963), GPSS III (1965), GPSS/360 (1967) és GPSS V (1971). Ezt a programnyelvet a szakemberek T. Schreiber monográfiájából ismerhették meg, ami 1980-ban jelent meg.
J. Henriksen. vezette be 1984-ben a GPSS első, a DOS operációs rendszer alatt futó GPSS/PC verzióját. Ezt fejlesztette tovább a Minuteman szoftver irányítása alatt S. Cox. A 20. század végén,1993-ban jelent meg a Minuteman szoftver forgalmazásában a GPSS World.
A nyelv leírása: A modell dinamikus eleme a tranzakció, egy absztrakt objektum, amely a statikus elemek között mozog, és egy valódi szimulált objektum különböző eseményeit újra előállítja. A modell működése során a szimulációs folyamat végén automatikusan létrejön a statisztika.
A modell statikus elemei: a tranzakciók forrásai, az eszközök, a várólisták (sorok) és mások. Elhelyezkedésük a modellben blokkokat határoz meg. A GPSS rendszert számos országban és az oktatási intézményekben is a gyakorlati feladatok megoldásához széles körben használják. A programozás nagyon egyszerű, kulcsszanak segítségével történik.
Példa a GPSS programkódra:

Megjegyzés: A programkódot kiemeltük, a megjegyzések a pontosvessző után olvashatók.
A bemutatott példa egy nyílt rendszert ír le. A szövödei kiszolgálás zárt rendszerben történik, mert a kezelt gépszám véges – amint ezt az előző részben elemeztük. A programot ehhez meg kell változtatni.
Egy zárt tömegkiszolgálási rendszer modellje: A kezelt 8 szövőgép átlagosan 0,6 óránként hibásodik meg. A szövő 0,12 óra alatt indítja azokat újra. A kód:

Vegyük észre, hogy ez az M/M/1//8 rendszer (1 kiszolgáló és 8 gép).
Ha a bemeneti folyamat nem véletlenszerű (exp), a második programsorba a bemenet paraméterezett eloszlásfüggvényét írjuk be. Így vizsgálhatók a különféle eloszlások a bemeneti oldalon.
Ha a szövő munkavégzési időtartama nem véletlenszerű (exp), hanem valamely másik eloszlásfüggvénnyel írható le, azt írjuk paraméterezve a hatodik sorba. Ezzel a kiszolgálási időtartam különféle eloszlásait vizsgálhatjuk.
Ilyen egyszerűen szimulálhatunk különféle, az exponenciálistól eltérő szituációkat. A program annyiszor fut le, ahányszor előírjuk, illetve annyi ideig fut, amely időtartamot megadunk neki.
A program alkalmazásához adott tehát a feladat: a leírandó rendszer bemeneti paramétereit meg kell határozni, úgymint
- a meghibásodások előfordulásának átlagértékét és eloszlását és
- a kiszolgálás időtartamának átlagértékét és eloszlását.
Ehhez a gyakorlatban az időmérésekkel előállított adathalmazokból készített hisztogrammok szükségesek. Ezzel közelítjük a valószínűségszámítás módszerével az eloszlásfüggvényeket.
A programban a hisztogram alapján a következő közelítő szabványos eloszlásfüggvények közül választhatunk (beépített eloszlásfüggvények):

A függvények paraméterezését lásd a program kézikönyvében. A szabványos eloszlásfüggvényeken kívül mód van az eloszlások hisztogramjának számpárokkal történő megadására is. Például egy exponenciális eloszlás a következő módon is megadható:
ХРDIS FUNCTION RN,С23 ; ехроnential distribution function
0.0/.1, .104/.2, .222/.3, .355/.4, .509/.5, .69/.6, .915/.7, 1.2/75, 1.38/.8, 1.6/.84, 1.83/.88, 2.12/.9, 2.3/.92, 2.52/.94, 2.81/ .95, 2.99/.96, 3.2/.97, 3.5/.98, 3.9/.99, 4.6/.995, 5.3/.998, 6.2/.999,7
Ezzel a módszerrel olyan eloszlásokat is vizsgálhatunk, amelyek semmilyen szabványos eloszlásfüggvénnyel sem írhatók le (pl. a lánc- és vetülék szakadások kijavítása időtartama két maximummal rendelkező eloszlását). Ha a kiszolgálási folyamat több, egymástól egyértelműen elkülöníthető folyamatból áll, a modell több csatornássá is alakítható és a modellezés e bonyolult rendszerrel is elvégezhető. Erre most itt nem térünk ki.
A program leírását lásd a forgalmazó által a programhoz adott leírásban (help). A GPSS program a leírásokkal együtt ingyenesen letölthető a http://minutemansoftware.com weboldalról.
Példák
A szövőgép kiszolgálásának modellezése
Amint arról említést tettünk, ez alkalommal a szövési munkaolyamat modellezésére teszünk kísérletet abból a célból, hogy bemutassuk a munkafolyamat egyes elemei közti valós összefüggéseket és ezen keresztül a folyamat lefolyását. A modell megváltoztatásával különféle szituációkat fogunk elemezni, s összehasonlítást teszünk az első közlésben bemutatott analitikus modellel, bemutatva a tevékenységünk eredményességét.
Mielőtt a bemutatást megkezdenénk, el kell készíteni a feladat megoldásának tervét. Az alábbi lépcsőket kell megjárnunk, hogy célhoz érjünk:
- A modellezés tárgyának elemzése.
- A matematikai modell kidolgozása.
- A GPSS Word programnyelvhez igazított általános algoritmus kidolgozása.
- A program-modell kidolgozása GPSS Word-ben.
- A program javítása („belövése”).
- A kísérlet előkészítése.
- A kísérlet elvégzése, értékelés.
Néhány szóban az egyes szakaszokban elvégzendő feladatokról:
- Az elemzés célja a végbemenő folyamatok azonosítása, azok paramétereinek meghatározása, az objektumon belüli hatások bemutatása. Először a kidolgozás csak szóbeli leírásra (közlésre) támaszkodhat. Ennek alapján kell meghatározni, mit kell modellezni, milyenek az objektumban a valós folyamatok, mik ezek közül a jelentősek, melyek hatását lehet elhanyagolni. Az összes fizikai folyamatot információs folyamattá kell leképezni. Meg kell határozni a be- és kimeneteket, a köztük lévő összefüggéseket. Ennek a folyamatnak az eredménye a folyamat blokkvázlatának az elkészítése.
- A működési modell a blokksémán alapul. Matematikai módszerekkel bemutatásra kerülnek azok a funkcionális átalakítások, amelyeket az objektumokon hajtunk végre. Ennek a lépcsőnek az eredménye a függvényekkel leírt működési modell. Egy ilyen modell lehet szerkezeti séma vagy működési rajz, amit különféle (szabványos és nem szabványos) grafikus elemekből építhetünk fel.
- Az algoritmus kidolgozása a GPSS nyelv alapfogalmai alapján történik (operátorok, szintaxis, programozási technika). A matematikai modellt át kell ültetni a program modell szerkezetébe. Itt már a program dokumentálásának egységes rendszerét kell alkalmazni, emiatt a szakasz eredménye a szabványos elemekkel ábrázolt algoritmus-szerkezet.
- A program kidolgozása az algoritmus elemenkénti pontosítása és átalakítása programszöveggé. A GPSS programozás-technikája különbözik más programnyelvekétől, itt ugyanis esemény-idő modellezést kell használni, össze kell vonni az objektum-orientált programozást a szerkezeti programozással. A lépcsőfok eredménye egy működőképes GPSS program szövege. Fontos, hogy a programsorokat megjegyzésekkel lássuk el. A programra ezek nincsenek hatással, de később segítenek a program javításában. A program modulok elhelyezkedése nincs hatással annak végrehajtására, elhelyezésüket a szövegben a programozási stílus határozza meg. A program végrehajtása az aktív tranzakciók mentén történik. Erről a lefordított belső program gondoskodik.
- A program javítása („belövése”) az esetleges hibák felderítésében és korrigálásában testesül meg. Ki kell dolgozni a javítás stratégiáját, a teszteket és a tesztelési folyamatot. Ennek a stádiumnak a végén működőképes, a modell-kísérletek végrehajtására alkalmas korrekt programot kell kapnunk. A „belövéshez” a GPSS speciális eszköztárát használjuk, ami magában foglalja, úgymint
- a lépésenkénti végrehajtást,
- a megjegyzések meglétét a sorok végén,
- az újságot (JOURNAL),
- az ablakokat (SIMULATION WINDOW, stb.) és
- a futás közbeni pillanatfelvételeket a program állapotáról (SIMULATION SNAPSHOT).
A programfutás végén megjeleníthető a szabványos jelentés (REPORT), amely információ elegendő ahhoz, hogy a modellezés eredményeit megismerjük és következtetéseket vonjunk le.
- A kísérlet előkészítése a stratégia és a taktika megállapítása. A stratégia megmutatja, hogy mi végre hajtjuk végre a programot, mik a be- és kimenő adatok. A taktika a kísérlet terve. A kísérlet célja a folyamat statisztikai jellemzőinek (a kihasználási tényező, az események eloszlási diagramja, stb.) meghatározása. Ki kell választani, hogy mely paraméterek állandóak és melyeket kell a kísérlet során változtatni.
- A kísérlet lefolytatása a következő:
- a program lefordítása GPSS nyelvre
- a GPSS ablakok kiválasztása a futás közbeni információ megtekintésére
- a bemenő adatok megadása
- a program elindítása (START, vagy egyéb módon)
- a szabványos jelentés kinyerése
- a kapott adatok rögzítése
- új kezdeti értékek meghatározása
- a program újra fordítása és újra indítása
- az adatok feldolgozása minden újra indítás után
- az eredmények analizálása, következtetések levonása
Az eredményeket file-ba írhatjuk, ezek az adatok más programok (pl. Word, Excel, stb.) segítségével is bemutathatók. A későbbi elemzés céljára az újságban (JOURNAL) és a SZABVÁNYOS JELENTÉSben található adatok megőrizhetők és átvihetők akár a szöveges jelentésekbe is.
Most pedig lássuk a konkrét feladatot! (Az elmélet átültetése a gyakorlatba)
Célunk a szövés munkafolyamatának elemzése. (Megjegyezzük, hogy a megállapításaink minden hasonló tömegkiszolgálási folyamatra is érvényesek.) Ebben a folyamatban két alapvető objektum vesz részt, a szövő és a szövőgép. Kevésbé fontos befolyással bír még a folyamatra a műszaki kiszolgálást végző mester és a hengercseréket végző segédmester vagy szerelő brigád. Első megközelítésben csak a szövő és szövőgép alkotta rendszerre koncentrálunk. Később a kevésbé meghatározó objektumok hatásával is foglalkozunk majd.
A kiválasztott objektumok együttműködése:
- A szövőgép szövetet állít elő. A szövőgépen feldolgozott anyagban (lánc- és vetülékfonal) lévő hibák miatt azonban ez a folyamat megszakadhat, mert a szövethiba megakadályozása végett a szövőgépet a hibát érzékelő berendezése megállítja.
- A szövő elhárítja a hibát (végteleníti az elszakadt fonalat, pótolja a hiányzó vetülék tartalékot, stb.), és újra működésbe hozza a szövőgépet.
Most azt az esetet vizsgáljuk, amikor ez a folyamat ismétlődik a munkavégzés teljes időtartamában.
A szövőgépek szerkezetének korszerűsítése és a rajtuk feldolgozott textilanyagok minőségének javulása azt eredményezte, hogy egy szövő több szövőgép kiszolgálását is el tudja látni. Így alakult ki a többgépes kiszolgálás, s jöttek létre olyan helyzetek, amikor a szövőgép leállásakor a szövő még a másik gép hibájának elhárítását végezte. Ilyenkor a gép várakozásra kényszerült, azaz várt a sorára. Ez a sorbanállás.
Ahhoz, hogy ezt a folyamatot mennyiségileg jellemezhessük, meg kell határoznunk, hogy a szövő hibák kijavítása által milyen mennyiségű szövetet képes előállítani a munkaidejében a. Ehhez ismernünk kell
- hány szövőgépet kezel a szövő
- mennyi a szövet előállításának a sebessége, ha a gép működik
- milyen gyakran szakad meg a szövőgép működése (áll le a gép).
A folyamat kimenete az előállított szövet mennyisége. Ha a folyamatot az időben vizsgáljuk, ennek egyenértéke a szövőgép(ek) időkihasználása (textiles terminológiával a „hatásfoka” – η) is. Kimenetnek tekintjük azt az időhányadot is, amit a szövő munkavégzéssel tölt. Ezt az időhányadot nevezzük terhelésnek (t). p0 az az időhányad, amikor a szövő tétlen.
A többi paraméter, a kezelt gépszám (N), a meghibásodások gyakorisága (λ) és a szövő munkavégző sebessége (μ) a bemenetek. (A jelölések megegyeznek a korábban alkalmazottakkal, lásd ott.)
A paraméterek meghatározásával felvázolhatjuk a rendszer működési modelljét.
Az egyes paraméterek közt matematikai összefüggések írhatók fel. Ha a korábban definiált
ρ = λ /μ
kiszolgálási tényező paramétert bevezetjük, az alábbi összefüggésekhez jutunk:
η = f1(N, ρ), illetve
t = f2(N, ρ).
Mind a λ mind a μ változók statisztikai mennyiségek, amelyek az időben változnak. Változásuk azonban egy átlagérték körül ingadozik. Ebben az esetben ezeket a statisztikai mennyiségeket várható értékükkel és sz az akörüli szórással jellemezzük.
Fontos paraméter még a középérték körüli eloszlás milyensége (függvénye).
A statisztikai mennyiségek jellemzőinek megállapítása az alábbiak szerint történik:
A középérték, amit a jelenségek észlelésének sorrendjében határozunk meg:

A szórásnégyzet ugyanilyen meghatározására a következő képlet szolgál:

Itt S a szórás számított értéke, σ a meghatározandó paraméter.
A fenti paramétereket kísérleti úton, úgynevezett szakadás felvétellel állapíthatjuk meg. Stopper órával több ezer adat regisztrálása után végezhetjük el a számításokat. Egy kézi programozható számológép segítségével a középérték és a szórás értékei az adatfelvétel során azonnal számíthatók a fenti képletek felhasználásával. A számított értékek ingadozása alapján dönthetünk a megfigyelés berekesztéséről. (A szükséges segédprogram elkészítése nem okozhat különösebb nehézséget.)
A két legfontosabb statisztikai jellemző megállapítása azonban egy kérdést még megválaszolatlanul hagy, az eloszlás jellegének megállapítását. Ehhez a felvételezett adatokból meg kell rajzolni a gyakorisági diagramot, s azt illeszteni kell a feltételezett eloszlás függvényekre. Ennek a tevékenységnek a leírása a statisztikai adatok feldolgozásának szakkönyveiben találhatók meg.
Néhány ilyen adatfeldolgozás során meggyőződtünk róla, hogy a beavatkozások időtartama leggyakrabban a logaritmikus normális eloszlásfüggvénnyel volt leírható. Ezt az eredményt a szakirodalom is alátámasztja, amely szerint a nagyon sok tényezőtől függő, összeadódó hatások következménye a lognormális eloszlás.
A lognormális és az exponenciális eloszlások vizsgálata
Tegyük kicsit részletesebb elemzés tárgyává a két felhasznált, a lognormális és az exponenciális (Markov folyamat) eloszlást. Az eloszlásfüggvények ábrázolásához szükséges hisztogramok előállításában is segítségünkre van a GPSS programnyelv.
A szimulációt 100 000 ciklus esetére végezzük el, hogy az elméletihez közeli eredményt kapjunk)
***A lognormális eloszlás paraméterei, képlete
***LOGNORMAL(Stream,Locate,Scale,Shape)
***Lognormális eloszlás, ahol Locate: λ=0.001, Shape: μ=1, Scale: σ=1
*** μ=1 és σ=1 a generáló normális eloszlás paraméterei
***A hisztogram készítés programja:
TT TABLE M1,.25,.25,20 ;0,25 kezdő érték és a lépésköz, ;20 adat
GENERATE (LOGNORMAL1,0.001,1,1)) ;lognormális eloszlás,
;λ=0.001, μ=1, σ=1
ADVANCE (LOGNORMAL1,0.001,1,1))
TABULATE TT
TERMINATE 1
START 100000
Az eredmény (a GPSS szabványos riportból):
GPSS World Simulation Report – tabulalas_lognormal
TABLE MEAN STD.DEV.
TT 4.488 6.149
A hisztogram: (lognormális)

Látható, hogy a, μ=1, σ=1 bemeneti paraméterek x = 4,488 (MEAN), s = 6,149 (STD.DEV) értéket adtak. Hogy összehasonlítható legyen az exponenciális eloszlásfüggvénnyel, az exponenciális eloszlás középértékét is 4,488-ra kell megadni.
(Megjegyzés: a programban a GPSS szabvány szerint tizedes pontot használunk)
A program:
***Az exponenciális eloszlás paraméterei, képlete
***EXPONENTIAL (Stream,Locate,Scale)
***Exponenciális eloszlás, λ=0 μ=σ=4.488 értékekre (az előző modellből)
TT TABLE M1,.25,.25,20 ;0,25 kezdő érték és lépésköz,
;20 adat
GENERATE (Exponential(1,0,4.488)) ;exponenciális eloszlás,
; λ=0 μ=σ=4,488
ADVANCE (Exponential(1,0,4.488))
TABULATE TT
TERMINATE 1
START 100000
A futtatás eredménye:
GPSS World Simulation Report – tabulalas_exp
TABLE MEAN STD.DEV.
TT 4.520 4.5
A hisztogram: (exponenciális)
Megjegyzés:
1. A szimuláció miatt ugyan eltérő értéket kapunk (4.488 bemenő, 4.52 kimenő átlagérték), holott az elméletileg ugyanannyi kellene, hogy legyen. Ez a szimuláció hibája.
2. A lognormális eloszlás szórása nagyobb, mint az exponenciálisé, ezért az összehasonlíthatósághoz a lognormális eloszlást tüzetesebb vizsgálat alá kell vonni.
A lognormális eloszlás vizsgálata
A normális eloszlás paramétereitől a lognormális eloszlás paraméterei eltérnek. Ezt az összefüggést ábrázolja az alábbi, a Wikipédiából átvett ábra.

A normális eloszlásfüggvénnyel azért kell foglalkoznunk, mert a GPSS programnyelvben a lognormális eloszlást a normális eloszlás paramétereivel definiálják:
LOGNORMAL (Stream,Locate,Scale,Shape)
Fogalmak jelentése:
- Stream a véletlenszám generátor száma (belső paraméter a program számára),
- Locate az x tengely mentén történő eltolás,
- Scale a generáló normális eloszlás középértéke,
- Shape a generáló normális eloszlás sűrűsége.
Az exponenciális eloszlással úgy lesz összehasonlítható a lognormális, ha a változó középértéke és a szórás is mindkét esetben megegyezik.
Miután a program a bemenetén a normál eloszlás paraméterét várja, át kell számítanunk a középérték és a szórás paramétereit, hogy a lognormális eloszlás kívánt középértékét és szórását kapjuk.
A paraméterek közti összefüggések (A lognormális paraméterek számítása a normális eloszláséból):
x = exp(μ+0,5σ2)+λ,
s = exp(2μ+σ2)*(exp(σ2)–1),
ahol
x – a lognormális eloszlás középértéke (E[X]),
s – a szórása,
μ és σ – a normális eloszlás ugyanazon paraméterei,
λ – az eltolás az x tengely mentén.
Ellenkezőleg, a lognormális eloszlás paramétereiből ki kell tudnunk számítani a normálisét, hogy az egyenlővé tehető legyen az exponenciáliséval. Ezek a paraméterek a fenti összefüggésekből képzett egyenletrendszerből átrendezésel, a megfelelő változók kifejezésével nyerhetők:
A levezetés:
ξ=x-λ
2lnξ=2*(μ+0,5σ2)=2μ+σ2
s/(exp(σ2)–1)= exp(2μ+σ2)=exp(2*lnξ)=ξ2
s=ξ2 *(exp(σ2)–1)
1+s/ξ2=exp(σ2)
ln(1+(s/ξ2)=σ2
2lnξ-2μ=ln(1+(s/ξ2)
2μ=2lnξ-ln(1+(s/ξ2)
Ennek alapján a kifejezett változók:
μ = ln(x-λ)–ln(1+(s/(x-λ)2))/2
σ = (ln(1+(s/(x–λ)2)))0,5
A szimulációs folyamat
A szimuláció folyamatát, a szabványos jelöléseket alkalmazva, a következőképpen ültetjük át a GPSS programnyelvre (a könnyebb érthetőség kedvéért alul magyarul is felírtuk az utasítások nevét):
Blokkvázlat:
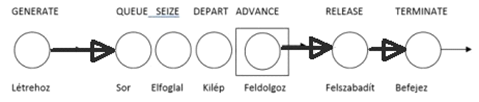
A programkód:
GENERATE 7,2 ;belép az igény a rendszerbe 7 min-ként +/- 2 min szórással (5-9 min)
QUEUE sor ;megnöveli a sor hosszát egy igénnyel
SEIZE csatorna ;megállapítja a csatorna foglaltságát
DEPART sor ;csökkenti a sor hosszát eggyel
ADVANCE 6,3 ;kiszolgálja az igényt 6 min átlagidővel +/- 3min szórással (3-9 min)
RELEASE csatorna ;felszabadítja a kiszolgáló csatornát
TERMINATE 1 ;kilépteti az igényt a rendszerből
START 200 ;200 ciklust hajt végre
A fent látható a legegyszerűbb kiszolgálási modell és annak GPSS nyelven megírt programja.
A szövő – szövőgép rendszer kicsit másképp működik, ugyanis több igényforrás van, s az igény a kezelt gépek bármelyikétől beérkezhet. A hibaelhárítás után a szövőgépet újra elindítja, s a szövő készen áll a következő beavatkozásra.
Emiatt a fenti nyílt rendszer helyett egy zárt rendszert kell létrehozni. Ennek blokkvázlata és programkódja:

A programkód
***SEGMENT 1
GENERATE ,,,8 ;a szövőgépek száma 8
;Itt nem határozunk meg az igényszámot, azt a kezelt gépek generálják
CIM ADVANCE(EXPONENTIAL(1,0,10)) ;véletlenszerűen 10 percenként áll le
QUEUE sor ;várnak a sorban a javításra
SEIZE szövő ;a szövő munkába veszi a gépet
DEPART sor ;kiveszi a sorból
ADVANCE(EXPONENTIAL(2,0,5)) ;véletlenszerűen 5 perc alatt javítja meg
RELEASE szövő ;befejezi a javítást
TRANSFER,CIM ;ugrása következő beavatkozásra
***SEGMENT 2
GENERATE 480 ;a munkaidő 480 perc
TERMINATE 1 ;a ciklus befejezése
START 1 ;indul az első tranzakció
A programot beírjuk a GPSS program szerkesztőjébe, majd futtatjuk. Végeredményként a szabványos riportban megkapjuk az eredményeket, ami – kivonatolva – az alábbi:
GPSS World Simulation Report – szoves_exp_exp
Sunday, March 29, 2020 15:57:46
START TIME END TIME BLOCKS FACILITIES STORAGES
0.000 480.000 10 1 0
…
FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER …
SZOVO 79 0.999 6.069 1 8 …
QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) …
SOR 7 6 85 1 5.121 28.920 …
Némi magyarázat a feliratokhoz (a bennünket érdeklő szavakat kivastagítottuk):
START TIME KEZDÉSI IDŐ A rendszeróra értéke a mérési időszak elején
END TIME LEÁLLÍTÁSI IDŐ Az óraidő, amikor a lezárási szám 0 lett.
FACILITY BERENDEZÉS A blokk neve vagy sorszáma.
ENTRIES BELÉPÉSEK száma
UTIL. A blokkban eltöltött idő hányada (szövő esetén ez a terhelés)
AVE.TIME Az egy benntartózkodás átlagos időtartama.
QUEUE SOR neve vagy száma
MAX CONT. A maximális sorhossz a szimuláció alatt
ENTRY A belépések száma
ENTRY(0) Azon belépések száma, amikor üres volt a sor.
AVE.CONT. A belépések számának átlaga.
AVE.TIME.QUEUE Az átlagos sorban állási (benntartózkodási) idő.
AVE.(-0) Ugyanaz az üres sorok nélkül.
A fentiekben csak példákat adtunk, amelyben a folyamatot illusztráltuk. A későbbiekben megelégszünk a szabványos riport adataival. Ezek (a riport jelöléseivel leírva):
A terhelés értéke közvetlenül leolvasható:
t = UTIL.
A hatásfok értékének meghatározásához az alábbi számítást kell elvégezni
η = (N*ENDTIME-(ENTRIES*(AVE.TIME+AVE.TIME.QUEUE))/N/ENDTIME,
ahol N a kezelt gépszám,
a többi megnevezés a GPSS program szabványos jegyzőkönyve szerint.
Ha idáig hibamentesen eljutottunk, belefoghatunk a kísérletezésbe.
A számított és a szimulált értékek összehasonlítása
Első lépésben elvégezzük a korábban levezetett elméleti modell és a szimuláció végeredményének egybevetését.
Első próba:
Az analitikus (Markov) modell (M/M/1//6)
N = 6 gép,
L = 1/λ = 15 min,
M = 1/μ = 1 min,
M/M/1//6 rendszer a fenti bemeneti adatok esetén a szövő tétlenségére p0 = 1 – t = 1 – 0,634 = 0,365 értéket adott.
A szimulációs programot 480 min időtartamra lefuttatva a M/M/1//6 modellre, a tétlenség p0 = 0,392 értékű.
Ha növeljük a futásidőt 1000 percre, p0 = 0,371 értékű lesz.
Ha 100 000 percre futtatjuk le a modellt, p0 = 0,365 értéket kapunk. Ez már megegyezik a számított értékkel.
Beigazolódott tehát, hogy az ismétlések számának növelésével a szimuláció pontossága növelhető, tehát szimulációval jól közelíthetjük az elméleti értéket.
A következő próba:
N = 5 gépre
L = 1/λ = 6,0 min,
M = 1/μ = 1 min értékekre
(M/M/1//5) analitikus számítással a modell p0 = 1 – 0,360 = 0,640 értéket ad.
Lefuttatva a szimulációt 480 perc futásidőre már p0 = 0,639 értéket kapunk.
100.000 perc futásidőre p0 = 0,640 értékű a tétlenség, tehát ugyanannyi, mint analitikusan.
- A következő lépésben összehasonlítjuk a különféle eloszlású kézi idők esetére a terhelés és a „hatásfok” (idő kihasználás) értékeit.
A számított eredmények a cikk elején közölt táblázatból az M/M/1//N rendszerre:
t = 1-p0 – a szövő terhelése
| ρ→ | 0,01 | 0,04 | 0,07 | 0,10 |
| N = 4 | 0,0396 | 0,1542 | 0,2579 | 0,3533 |
| N = 6 | 0,0594 | 0,2288 | 0,3820 | 0,5155 |
| N = 8 | 0,0792 | 0,3037 | 0,5010 | 0,6617 |
η – a hatásfok
| ρ→ | 0,01 | 0,04 | 0,07 | 0,10 |
| N = 4 | 0,9900 | 0,9638 | 0,9211 | 0,8833 |
| N = 6 | 0,9900 | 0,9533 | 0,9095 | 0,8592 |
| N = 8 | 0,9900 | 0,9491 | 0,8946 | 0,8271 |
A szimulált eredmények (M/G/1//N) rendszerre (ahol G – lognormális eloszlás)
Szimuláció 480 percre, egy műszak idejére.
Az adatok pontossága a szimuláció miatt csak hozzávetőleges:
t= UTIL.
| ρ→ | 0,01 | 0,04 | 0,07 | 0,10 |
| N = 4 | 0,062 | 0,253 | 0,370 | 0,487 |
| N = 6 | 0,075 | 0,342 | 0,515 | 0,644 |
| N = 8 | 0,116 | 0,428 | 0,650 | 0,818 |
η = (N*END TIME-(ENTRIES*(AVE.TIME+AVE.TIME.QUEUE))/N/END TIME
| ρ→ | 0,01 | 0,04 | 0,07 | 0,10 |
| N = 4 | 0,983 | 0,928 | 0,884 | 0,837 |
| N = 6 | 0,986 | 0,931 | 0,882 | 0,826 |
| N = 8 | 0,985 | 0,927 | 0,864 | 0,761 |
Látható, hogy az adatok eltérőek. Ugyanazon kiszolgálási tényezőhöz lognormális eloszlás esetén nagyobb terhelés érték tartozik.
Ez azt jelenti, hogy
- ugyanazon terhelés mellett kisebb kiszolgálási tényező érhető el, vagyis
- ugyanazon szakadékonyság mellett nagyobb a szövő terhelése.
A konkrét szituáció vizsgálata nagyon sok részletkérdés megvizsgálására alkalmas. Ezek közül csak néhányat villantottunk fel.
Végkövetkeztetések, zárszó
A szimuláció segítségével olyan körülmények is vizsgálhatók, amelyek analitikusan nem írhatók le.
Ha a dolgok természetét vesszük górcső alá, a beavatkozások több csoportba oszthatók. A következő táblázat ezt a csoportosítást mutatja be.
| A leállás oka | Az elhárítást végzi | Gyakoriság | Időtartam |
| Láncszakadás | szövő | 3 – 20 percenként | 2 – 7 perc |
| Vetülék szakadás | szövő | 2 – 20 percenként | 1 – 3 perc |
| Vakleállás | szövő | 10 – 50 percenként | 1 – 2 perc |
| Darabvétel | szövő | tervezhető | 5 – 10 perc |
| Lánchenger csere | segédmester, szerelő | tervezhető | 250 – 500 perc |
| Javítás | mester, lakatos | 400 – 800 percenként | 60 – 500 perc |
Egyéb veszteségidő (anyag, energia, munkás hiány, stb.) nem tervezhető.
Amint látható, az eddigi vizsgálatba a lánc-, vetülék szakadásokat, a vakleállásokat, esetleg a darabvételt vonhattuk be. A konkrét szakadásfelvételek alapján külön-külön eloszlás-hisztogramokat is felrajzolhatunk.
Az, hogy az egyes hibaokok aránya milyen, a körülmények függvényében változik. Ideális esetben az okonkénti időtartamuk olyan elegyet alkot, hogy egy eloszlásnak tekinthetjük az egész folyamatot. Ebben az esetben van lehetőség statisztikai módszerekkel elméleti eloszlásfüggvényeket illeszteni a hisztogramokra.
Előfordulnak azonban olyan esetek is, hogy a különféle ok miatti beavatkozások egyesített hisztogramja több maximumot is tartalmaz, vagy alakja szabványos eloszlásfüggvénnyel nem közelíthető. Erre az esetre ad a GPSS program olyan lehetőséget, hogy a gyakorisági diagramot pontok sorozatával adjuk meg. (Egy példát korábban bemutattunk)
Lehetőség van többcsatornás modell megalkotására is, ahol minden csatornának saját eloszlásfüggvény adható meg, s meghatározható a csatornákon áthaladó tranzakciók aránya is.
Ezzel a témával terjedelmi okokból itt nem foglalkozunk. Akit a téma mélyebben érdekel, ajánljuk a programnyelvvel kapcsolatos, a forgalmazó által elkészített, alapos programleírást és a szakirodalomban fellelhető rengeteg példát.
Megjegyezzük továbbá, hogy a szimuláció az ipari és egyéb területeken széleskörűen felhasználható a folyamatok leírására. Csak felsorolásképp:
- a számítógépek belső adatfolyamának megtervezésénél,
- a szerelési, építési munkaszervezésnél,
- a szolgáltatás és
- az egészségügy területén és még sok helyütt.
Célunk a módszer ismertetésén túl az alkalmazhatóságának a bemutatása volt – a textiliparban.
Ajánlott irodalom:
Tankönyvek:
- Кудрявцев Е. М. GPSS World. Основы имитационного моделирования различных систем. – Москва ДМК Пресс, 2004.
- Матюшенко С.И., Спесивов С.С. Основы имитационного моделирования в среде GPSS World М.: Изд-во РУДН, Москва 2006
- С.С. Смородинский, Н.В. Батин Оптимизация решений на основе
компьютерных имитационных методов и моделей, БГУИР, Минск 2005 - Титоренко М.В., Баженов Р.И. Об имитационном моделировании систем
массового обслуживания в среде GPSS 2014. - http://naukarastudent.ru/11/2134/
Szakcikkek:
- Thomas J. Schrieber szakcikkei bőséges irodalomjegyzékkel (Thomas J. Schriber
- Graduate School of Business The University of Michigan Ann Arbor MI 48109-1234 USA)
Példák GPSS megvalósításokra:
https://www.researchgate.net/publication/281861420
https://www.matburo.ru/ex_mat_pr.php?p1=gpss
Szerző:
Prátser András, Rejtő Sándor Pro Technológia Alapítvány a Könnyűiparért